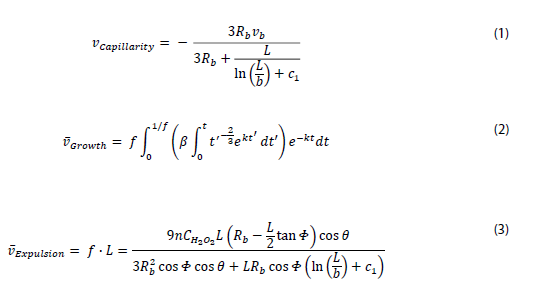Miniaturization can be considered as the main driving cause for the tremendous technological advances within the last decades. Besides smaller and faster mechanical and electrical devices, scientists engineered new machines at the micro- and nanometer scale also referred to as micro-/ nanomotors, -swimmers or -robots. While the small-scale mechanical and electrical devices already revolutionized all industry sectors, the latter mentioned micromachines are still missing impactful real-world applications. Due to their small size, micromachines are cost effective, resource conserving and capable of reaching narrow passages and niches. These are important advantages in terms of resource shortage and sustainable developments. Nevertheless, non-intuitive physics at small scales make designing such micromachines an arduous endeavor. Therefore, a fundamental understanding and modeling of the underlying concepts for the actuation, propulsion and interaction of micromachines with their surroundings is crucial to validate their potential to revolutionize several sectors such as microrobotics [1,2], microfluidics [3-5], medicine [6-8] and environmental remediation [9-11].

In the course of this commentary, we aim to discuss the need of physical models supported by experimental data that can facilitate the translation of micromachines into realworld applications. Here our previous paper on modeling the propulsion mechanism of conical chemical-propelled micromotors [12] is selected as a case of study for our discussion. In that paper, we investigated the physics of motion of 50 μm long conical micromotors under changing viscosities, fuel- and surfactant concentrations. Our results revealed a previously unknown switching of propulsion mechanisms and led to a new, more accurate, physical model.

Systematic experiments to unveil the propulsion mechanisms for micromotors

Reproducible and reliable results are crucial for systematic experimental studies, to allow comparisons between each acquired data set. Hence, important experimental parameters need to be identified and deviations kept minimal. In our particular study [12], the main experimental factors were already unveiled by previous studies [13-17]. These were the fuel concentration, surfactant concentration, viscosity of the fluid and geometry of the micromotor. Consequently, deviations in fluid composition and in fabrication of the microrobots should be minimal. Therefore, we used three dimensional (3D) two-photon laser lithography as the fabrication method for our micromotors. This technology allowed for precise, high-resolution printing of versatile microscale geometries [18]. All needed chemicals were prepared in large amounts. Consequently, all experiments could be carried out with the same batch. This minimized deviations in the chemical composition.

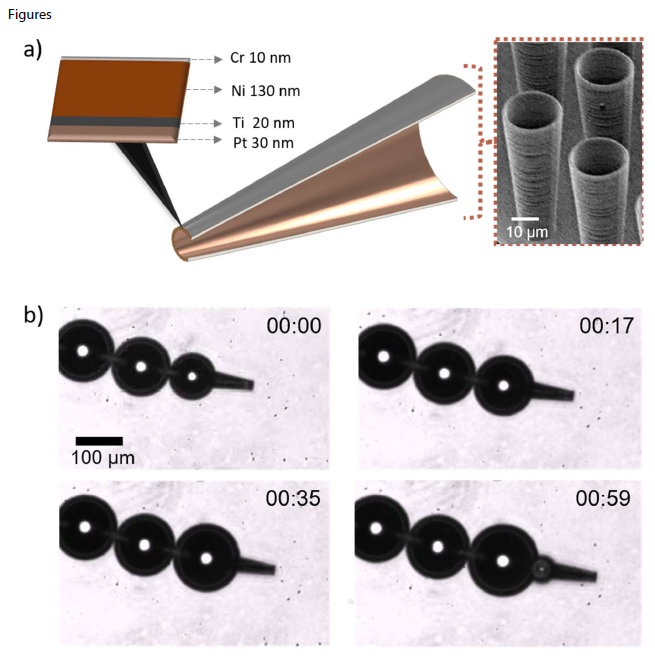
In our study, we decided to keep the geometry of our micromotors constant throughout all experiments to emphasize the importance of the fluid composition on the hydrodynamics of this particular micromotor type. The used cone-shaped micromotors had a length of 50 μm and a semicone angle of 5°, resulting in a large opening with a radius of 10 μm. A coating with Cr (10 nm), Ni (130 nm), Ti (20 nm), and Pt (30 nm) by e-beam evaporation (Edwards E-Beam) was applied (Figure 1a). The Pt formed the outer layer inside the tube cavity to serve as catalytic surface for the chemical reaction necessary for propulsion. A magnetic guidance was possible due to the Ni nanofilm deposited on the outer surface. These micromotors were immersed into fluids with alternating concentrations of hydrogen peroxide (H₂O₂), sodium dodecyl sulfate (SDS) and methylcellulose (MC).

Figure 1: Structure and motion of conical chemically propelled microrobots used for experiments. a) Schematic half-cut depiction and SEM image of conical micromotors. As presented in the sketch the micromotors were coated with 10 nm Cr, 120 nm Ni, 20 nm Ti and 30 nm Pt. The Pt as outer layer serves a catalytic agent to induce the chemical reaction required for propulsion. b) Microscope images of a micromotor moving inside a 2.5% H₂O₂ (v/v) and 5% SDS (w/v) solution. The growth and expulsion of the bubbles is clearly visible. The whole motion is tracked over a time course of 00:59 sec. The microscope and SEM images are adapted and reproduced with permission from [12].

Here H₂O₂ served as fuel for the micromotors. The energy required to propel catalytic micromotors was provided by the decomposition of the surrounding H₂O₂ fuel into oxygen gas O₂, which was catalyzed by the inner Pt layer of the tube. The O₂ formed bubbles inside the conical tube. Due to the asymmetry of the conical tube, the continuously growing bubble moved towards the larger tube end, were it got expelled. This whole process led to a motion of the microrobots as depicted in Figure 1b. An increase in H₂O₂ concentration led to an increased O₂ production rate, thus enhanced bubble growth and bubble expulsion frequency. Concentrations of 2.5%, 3.75%, 5%, 7.5%, 10%, 20%, and 30% (v/v) H₂O₂ and constant 5% (v/v) SDS were used. Wholesome this resulted in higher propulsion speeds. SDS acted as a surfactant reducing the surface tension of the fluid. This allowed the bubbles to move through the tube faster and detach easier from the tube opening. Here we used concentrations of 1.25%, 2.5%, 5%, 7.5%, 10%, 20%, and 30% SDS (w/v), with constant 2.5% H₂O₂ (v/v). Additionally, we varied the viscosity of the fluid by altering the concentration of MC. Higher MC concentrations increased the viscosity, and hence the drag force acting on the micromotors. In our investigations, we used 0%, 0.05%, 0.1%, 0.15%, 0.2%, 0.25%, 0.4%, and 0.6% (w/v) MC, corresponding to fluid viscosities of 0.0013, 0.0018, 0.002, 0.0022, 0.0025, 0.0028, 0.004, and 0.006 Pa.s. The H₂O₂ and SDS concentrations were kept constant at 2.5% (v/v) and 5% (w/v), respectively, offering the best motion stability.

Analysis and modulation

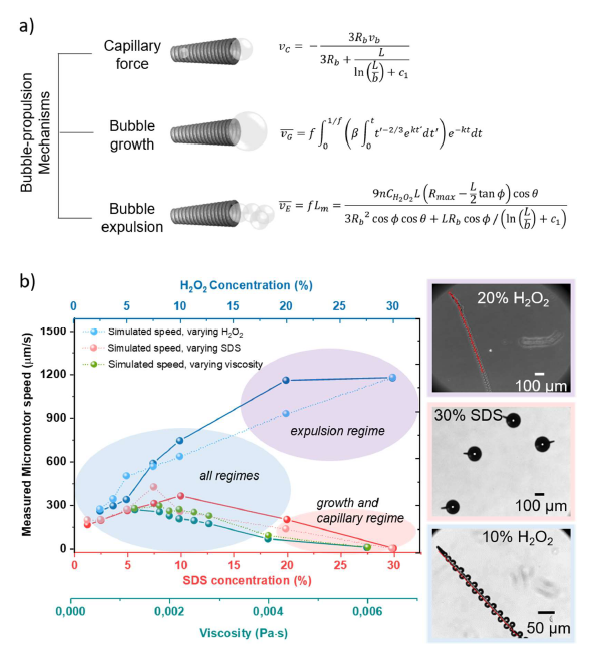
To quantify the change in motion behavior of our microrobots in the presence of different fluid conditions, different parameters were analyzed. We measured the bubble radius and expulsion frequency as well as the micromotor`s speed. This was done using the image processing program ImageJ. Additionally, we compared our results with the values predicted by the already established models (Figure 2a) referred to as capillarity [19] (Equation 1), bubble growth [20] (Equation 2), and bubble expulsion [21] (Equation 3). The velocity v according to each model is:

Figure 2: Depiction of different physical mechanisms contributing to the micromotors motion under various conditions. a) Schematic representation of the different propulsion mechanisms and the corresponding average micromotor speeds. From top to bottom the capillary force mechanism, bubble growth and bubble expulsion mechanism are presented. b) Measured fluid-composition-dependent speeds of the micromotors (full lines). Additionally, the simulated speed according to the different propulsion models is plotted (dashed lines). The analysis of the experimental data showed a switching of propulsion mechanisms. The dominant propulsion regimes for given fluid conditions are indicated in the graph. The expulsion regime is dominant for the H₂O₂ concentrations above 20%, illustrated in violet. The SDS concentrations of 20% and higher as well as the viscosities starting from 4 mPa.s show dominance of the growth and capillary regimes (pink area). All three regimes coexist for the remaining fluid conditions (blue area). Exemplary microscope images for each propulsion regime are depicted next to the graph with the corresponding color coding. All graphs and images are reused and adapted with permission from [12].

R_b, v_b, f, L are the maximum bubble radius, bubble velocity relative to the tube, the bubble expulsion frequency and length of the micromotor respectively. The factor b is defined by 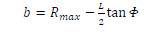 with the larger tube opening radius R_max and the semi-cone angle Φ . The time, H₂O₂ concentration and the inclination angle of the bubble speed with respect to the inner wall of the tube are denoted by t, C_H2O2 and θ. Here the parameter n is taken from experiment. For calculation of the parameters c₁, β, and k we refer the reader to our paper [12].

These three models individually could not explain our observations. A more detailed analysis of our videos revealed a switching of propulsion mechanisms depending on the fluid composition. In particular, a dominant influence of the bubble growth was attained for the concentrations higher than 20% SDS (at 2.5% H₂O₂) as well as for the concentrations of 0.4% MC (w/v) and higher (with viscosity above 0.004 Pa.s) at 2.5% H₂O₂ (v/v) and 5% SDS (w/v). The bubble expulsion dominated the propulsion at 20% (v/v) and higher concentrations of H₂O₂. We therefore decided to unify the three propulsion models treating them as separate mechanisms contributing to the propulsion of the micromotors as a single whole. The timeaveraged velocity v of the micromotor is given by:

where v(t) and 1/f are the instantaneous velocity of the micromotor and the time period between two consecutive bubble ejections. The new unified model (Equation 4) described the micromotors’ speed more accurately, as illustrated in Figure 2b. Further on, we used this model to predict the influence of varying geometric parameters on the micromotors propulsion. Specifically, 50 μm long micromotors with the varying semi-cone angle (2.5°, 5°, and 10°), as well as micromotors with a semi-cone angle of 5° and varying lengths of 25, 50, and 100 μm, were modelled. Our model predicted a slight increase of the drag force and an increase of all driving forces with the semi-cone angle or the length. This resulted in an increased propulsion speed for larger lengths and smaller semi-cone angles. Overall, the obtained results were in good agreement with experimental evidence [14]. However, a further study providing experimental data at varying the above-mentioned geometrical parameters is necessary to confirm the model-based predictions.

The systematic experimental study of the mechanisms influencing chemically bubble-propelled conical tubular micromotors provided new insights into the underlying physics of motion at low Reynolds number. Our study revealed a switching of propulsion mechanisms in dependence on the fluid composition. To describe this behavior, none of the established models individually was sufficient, but rather a combination of all three models was needed. Consequently, these three models can be described as mechanisms contributing to the micromotors’ speed as a single whole. The developed model could precisely predict the speed of micromotors under various conditions. However, some improvements could be provided by the further studies. In the course of our experiments, we tested 20 micromotors each in 20 different fluid conditions. Even though a large number of parameters was considered, still larger data sets would provide more robustness to the model. Additionally, our model does not consider an eventual influence of the magnetic force acting on the microrobots during its guidance. Even though we positioned the magnet as far as possible from the micromotors and only measured the speed after the microrobots were aligned to one direction, there might be a magnetic force contributing to the micromotors speed. When operating in viscous media, or due to the expulsion of bubbles, we have observed a wobbling effect, which might be partially corrected by an external magnetic guidance. Similar phenomena are known for helical micromotors or biohybrid micromotors where side-wise motions can be corrected due to the presence of a magnetic field. Consequently, for some applications, e.g., in medicine, where precise magnetic guidance is needed [22], a consideration of the magnetic force would be important. Another crucial parameter to consider is the geometry of the micromotor. Depending on the environmental conditions, parameters such as the length, the semi-cone angle and the surface roughness must be accounted for. Therefore we used our model to predict the behavior of chemically propelled conical micromotors with varying length and semi-cone angles [12]. Still, these predictions need experimental proof. Such experimental data would help to further enhance the precision and robustness of predictions made by the model. Overall, our study serves as an example of the cruciality of experimental-data-supported physical models for the propulsion of micromachines.

To this point, only few studies systematically the physics of motion of micromachines by developing new, precise, and robust models. A greater emphasis on such studies might shed new light onto the highly complex and unintuitive physics at small scales. As in our case, this could lead to the discovery of new fascinating phenomena. Of course, crucial influencing physical or chemical parameters have to be identified first by preliminary experiments to enable such a study. But for many types of micromachines, such parameters were already unveiled and published by the community.

Additionally, the fundamental understanding of micromachine motion physics and their interaction with the environment could serve as a basis to design highly adapted and optimized micromachines for various applications, especially in complex scenarios, such as, for medical interventions in the human or animal body.

Many promising micromachines for various high impact applications were presented within the last years. However, no commercial application of micromachines is available yet. This is mainly caused by big challenges that researchers face when translating their research into real-world scenarios. In particular, the small size of these devices leads to highly unintuitive physical motions and makes it hard to visualize them otherwise than with a microscope. But for the most impactful applications, which emerge in the field of medicine, microscopes are not a suitable imaging modality. Such medical applications could include the targeted delivery of cargos [23-25], blood clot removal [26,27] or assisted fertilization [28,29]. In all these scenarios, the micromachines face highly complex and versatile environments. A precise control of the microrobots is necessary to avoid unwanted and potentially severe side effects. We believe that precise and robust physical models of the micromachines behavior may play an important role for successful translation from bench- to bedside. Turning such models that are supported by experimental data into programs might serve researchers as an important tool. It could help to optimize and predict the behavior of micromachines within different given scenarios. The models could also be used to produce artificial data sets and add these to the already existing data. The resulting big-data sets could be used for advanced analysis tools such as artificial intelligence (AI). The AI may find even more unintuitive and mathematically hard-to-describe phenomena. Another way to achieve larger data sets with real experimental data would be the establishment of a global open-source database, where all researchers can upload and receive data sets of given types of micromachines to advance physical models. Also, the program could be used to find the optimal micromotor geometry for given fluid parameters or vice versa, without time-consuming experiments. Additionally, a reliable prediction of the micromachines’ behavior would allow for a more precise imaging and tracking in-vivo. This, in turn, could overcome the abovementioned challenges when translating micromachines into meaningful real-world applications.

We therefore encourage our community to put a stronger emphasis on such systematic physical studies to develop new fascinating models that could bring micromachines to new horizons.

P.W. thanks the Max Planck Society and the Max Planck and ETH Center for Learning Systems for the financial support. The underlying research was funded by the German Research Foundation SPP 1726 “Microswimmers – From Single Particle Motion to Collective Behavior and by the Leibniz Program of the German Research Foundation (SCHM 1298/26-1). V.M.F. acknowledges partial support through the MEPhI (Russia). This work has been partially funded by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement nos. 835268 and 853609).

All authors contributed to conceiving, writing and revising the manuscript.

The authors declare no competing financial or non-financial interests.