Abstract
Introduction: Despite a wide range of applications of robotics in medical sciences, the role of medical robotics in orthopedic surgeries is of great importance.
Methods: In the present study, the transformation, spatial description, and movement of the Yaskawa Motoman MH5 robot were compared with two improved types of this robot. In type A, a rotational joint is replaced with the prismatic joint, and in type B, beside a rotational joint, a prismatic joint is added to the mechanism of the original robot.
Results: The results demonstrated that despite the fact that type A used less distance, it had a stronger possibility than type B for workspaces feasibility spatial movement. The results also indicated that the first, second, and third joints must be involved to create a static balance in type A robot, and for type B, in the same conditions, the first, second, third, and fourth joints must be involved. This means that the type A robot needs a higher power to make the balance, and the error potential in the type B robot is higher than that of type A.
Discussion: The internal loading that the joints of type A robot must tolerate maintaining a static balance is greater than that of type B, which causes more wear out of type A robot. From workspaces and movements points of view, the efficiency of the type B MH5 robot is greater than in other cases.
Keywords
Medical robotics, Orthopedic surgery, Spatial description, Joint movement, Yaskawa Motoman MH5, Work space, Force
Introduction
Using robots in surgeries dates back to the mid-1980s [1]. The robotic was applied in a wide range of biological and medical sciences such as clinical medicine [2-5], neuroscience [6-15], cardiovascular [16-20], dentofacial [21,22], and cellular and molecular life sciences [23,24]. Orthopedic robots are much more widely used and complex in medical engineering sciences [25]. Recently, due to the promising results in the short-term recovery of patients, utilizing robotics in orthopedic surgeries has significantly increased compared to traditional orthopedic surgery methods [25]. For instance, technological innovations in uni-compartmental knee replacement (UKR) surgery robots allow surgeons to plan preoperatively and perform it during the surgery with the highest accuracy. Current fields of orthopedic robotics focus on a variety of hip joint surgeries such as femur preparation, acetabulum placement, and pelvic and femur osteotomies. In knee surgeries, robotics can be used in total knee arthroplasty, anterior cruciate ligament reconstruction, and arthroscopy. Robots in orthopedic surgeries are generally divided into three categories: automatic, haptic, and passive surgery systems.
Robodoc is the oldest and first automated robot used in orthopedic surgeries. The disadvantages of automated robots in orthopedic surgeries include the difficulty of designing an engineering system that is capable of interacting with soft tissues, which can move and change shape during the surgery. Utilizing these types of robots in orthopedic surgeries also increase the rate of nerve damage and infection. The many problems posed by using automated robotic systems in orthopedic surgeries have led surgeons to use haptic robotic systems.
The robotic arm interactive orthopedic system (RIO) that is generally used in UKR surgeries is the most famous haptic robot. In addition, the use of this robot is also very common in computed tomography (CT) images to create a three-dimensional model of the patient’s skeleton. It allows the surgeon to perform the surgery by making a smaller incision, which in turn helps short-time recovery for patients. Utilizing the haptic system uni-compartmental knee replacement has eliminated many of the disadvantages of non-robotic knee joint surgeries. These systems help increase the accuracy of component alignment and create a better balance in ligaments. Roche et al. studied 344 patients who used RIO in knee replacement surgery and reported that 3% of the patients suffered from postoperative complications, indicating promising results in using this system [26]. Acrobat system is another type of haptic robot that was used in biomedical robotics. Cobb et al. compared UKRs with and without the Acrobat system [27]. The results of this study showed that the angle between the hip and the femur in the Acrobat system is less than 2 degrees, while in the surgery without the help of these robots, only 40% of patients had an angle of fewer than 2 degrees. Although there were a few reports about the application of Acrobat surgery in biomedical robotics, however, these limited short-term data revealed the acceptable outputs of these types of robots.
Computer-assisted or computer navigation surgery systems, also called passive surgery systems, monitor progress and provide surgeons with data during procedures. These systems are used peri-operatively: 1) to assess joint irregularities and joint biomechanics; 2) to make recommendations on how to continue with the procedure, when assessing ligament balancing, for instance; and 3) to monitor the accuracy of the bone cuts. Passive surgery systems provide detailed information to the surgeon, who always has the option to override the system’s suggestions. Passive systems also provide assistance to surgeons during UKR by facilitating more accurate radiological placement of the components. Musahl et al. indicated that the computer-guided navigation enabled component positioning to within 2° of the pre-operative plans in all cases [28]. The results of previous studies showed that passive surgery systems can play a prominent role in progressing the quality of biomedical robotics.
Despite all of these developments in biomedical robots, a new approach to approved robotic systems to replace stereotactic frames. They excel at using spatial information, have more flexibility to follow paths, even in unusual paths, and can have a simple and user-friendly interface with a tireless and very accurate mechanism. Moreover, their sturdy structure allows them to assist surgeons in various parts of orthopedic surgeries, especially in bone drilling and controlling the drill direction and the drill depth. Since bone drilling is one of the high-sensitive parts of orthoptic surgeries and paying attention to increasing the quality of these procedures is highly valuable from the clinical viewpoint [29,30].
The power to drive a robot, error potentials in the function of the robots and movement feasibility are the important parameters to increase robot efficiency. On the other hand, in plate or implant insertion and advance drilling operations, a robot needs a combination of rotational and prismatic joints in order to make optimal workspace and increase work efficiency. Accordingly, the present study attempted to improve the efficiency of the Yaskawa Motoman MH5 industrial robot for utilizing in orthopedic surgeries by making a change in joints and the degree of freedom of this robot.
Materials and Methods
Given the main purpose of the research, the joints and arms of the Yaskawa Motoman MH5 robot were modified and 2 different robots with prismatic motion, named type A and type B, were modeled and compared with each other. The mentioned Motoman robot has 5 rotating joints and 2 main arms.
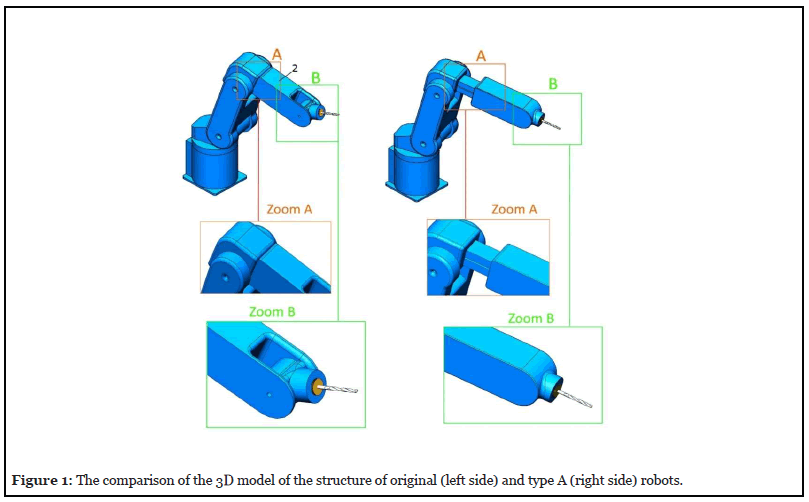
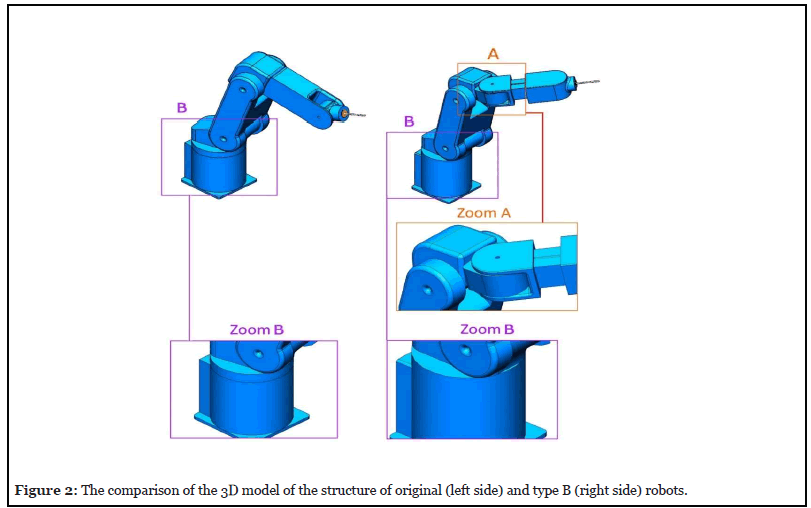
In type A, a rotational joint is replaced with the prismatic joint before the end effector. In type B, besides a rotational joint before the end effector, a prismatic is added to the mechanism of the original robot. To solve this problem in type A robot, as shown in Figure 1, a prismatic joint was placed within arm 2. But this prismatic movement is useful only when the end effector is in the same direction as arm 2. Thus, according to Figure 1; zoom B, the rotating joint between the end effector and arm 2 was removed and the two links were joined to each other in the same direction. For the type B robot, according to Figure 2, in addition to the prismatic joint, two rotating joints were also added to arm 2, one on the x-axis and the other on the y-axis. Since joints 2 and 0 do the same rotations, as shown in Figure 2; zoom B, joint 0 in type B was removed. These changes in robot B aims at increased access to the workspace of the operation and reduced access to points that are not used in the operation. The two robots were eventually compared in order to identify the robot with higher efficiency. It should be noted that the CATIA V5-6 R2017 SP6.0/2018 software was used to create the three-dimensional models of the robots. The Matlab V2019 software was used to calculate the matrixes and analysis the results. It is worth mentioning that in the present study, the simulation results of displacement, movement and forces of two new types of the Yaskawa Motoman MH5 robot were compared with this original robot.
Results and Discussions
Transformation and spatial description
The degrees of freedom and the size of the robot allow it to have access to the required points in the surgical workspace. Its main task is to follow a predetermined path in order to move the drill or the probe in a certain direction. But because it does not have a prismatic joint in its end effector, it needs to use several joints simultaneously to perform the operation, which results in reduced efficiency of the robot.
Forward kinematic analysis is an important analysis to describe the transformation and displacement of a robot.As a result, the Denavit-Hartenberg (D-H) parameter table was first calculated for both types of robots (Tables 1 and 2).
| i | i-1α | ai-1 | di | θi |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | θ1 |
| 2 | -90 | 88 | 0 | θ2 |
| 3 | 0 | 310 | 0 | θ3 |
| 4 | 90 | 0 | D4 | 0 |
| 5 | 0 | 0 | 0 | θ5 |
Table 1: The Denavit-Hartenberg parameters for type A Robot.
| i | i-1α | ai-1 | di | θi |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | θ1 |
| 2 | 0 | 310 | 0 | θ2 |
| 3 | -90 | 0 | 114 | θ3 |
| 4 | 90 | 0 | 0 | θ4 |
| 5 | 90 | 0 | D5 | 0 |
| 6 | 0 | 0 | 0 | θ6 |
Table 2: The Denavit-Hartenberg parameters for type B Robot.
The transformation matrix obtained from Equ.1 is a combination of R3 × 3 and P3 × 1 matrices [31,32], which were calculated for both type A and B via the forward kinematic method.

In these calculations, Sθ and Cθ represent Sin (θ) and Cos (θ), respectively, and the center of the brain is considered as the origin of the coordinates. Therefore, the spatial position of the final destination of the end effector for each type of robot was considered in the same conditions and in the position [10, 5, 5]T (units are in mm). Then, the spatial location of the initial origin of types A and B in equations 4 and 5 were compared. To achieve the same position for the end effector of both types of robots, type A, with [1o, 41o, -29o, 100mm, 0o]T [θ_1, θ_2, θ_3, d_4, θ_5,]T input, and type B, with [41o, -29o, 90o, 1o, 100mm, 0o]T [θ_1, θ_2, θ_3, θ_4, d_5, θ_6,]T input, were compared. The results showed that the initial positions of type A and type B were x = 29.5536, y = 5.5075, z = 81.9142 and x = 104.6077, y = -81.7709, z = 11.8170 mm (Equations 4 and 5), respectively. Given these relations, the distance traveled by type A and type B to reach a shared destination was 87.25 and 133.30 mm, respectively. Therefore, despite the fact that type A used less distance, it had a stronger possibility than type B for spatial movement and transformation.

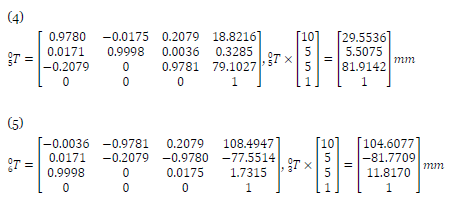
The Jacobian Matrix
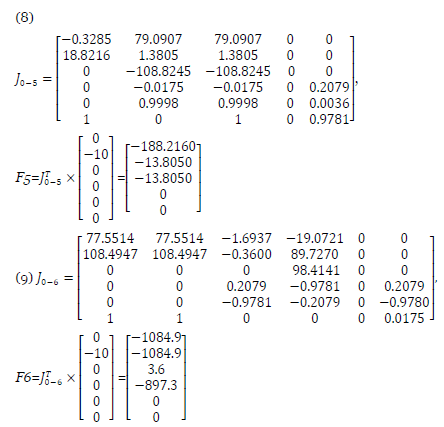
To evaluate and compare the balance of the two robots, the inputs of their joints were analyzed and their condition was compared in this regard. To this end, the Jacobian matrix was calculated for the two robots. This matrix consists of 6 rows and the number of columns is equal to the number of the intended robot’s joints. The first three rows (JV) are derived from P3 × 1 matrix relative to the joint variables (q), and the second three rows (Jω) are obtained using R matrices of each joint relative to the other joint. Equations 6 and 7 show the Jacobian matrix for type A and type B robots, respectively.

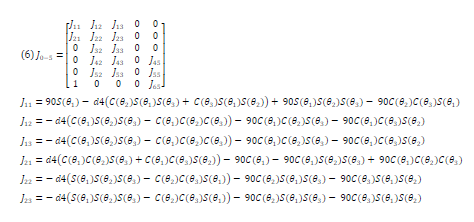


Then, taking into account the drill weight for both types of robots, the external loading was calculated. Given the normal weight of the drill, this number was considered 0N1, so that the balance of both robots can be compared in the same conditions. Thus, the external loading matrix for both robots was considered [0, 10N, 0]T. Then, by multiplying the transpose of the Jacobian matrix for type A and type B robots by the external loading matrix, the results of the joints’ inputs are calculated in Equations 8 and 9, respectively. The results showed that the matrices of the joints’ inputs of type A and type B robots to create a static balance was [-188.21, -13.8050, -13.8050, 0, 0]T and [-1084.9, -1084.9, 3.6, -897.3, 0, 0]T, respectively.
This means that the first, second and third joints must be involved to create a static balance in type A robot, and for type B, in the same conditions, the first, second, third, and fourth joints must be involved. The internal loading that the joints of type A robot must tolerate maintaining a static balance is greater than that of type B, which causes more wear out of type A robot. If the vibration conditions are not designed properly, in the future, the robot may encounter various errors during surgeries. Since orthopedic surgeries require great care and need to be performed with high sensitivity, this loading difference may cause irreparable damages to patients.

Clinical approach
In patients undergoing plate or implant insertion and joint replacement surgeries, and in bone drilling operations during orthopedic surgeries, the accuracy of the surgical procedure is of great importance. The improper surgeries and the consequent failure in the process may lead to an inadequate healing process, fatigue increase, and postoperative problems [25, 29]. One of the effective methods to increase the accuracy and improve outcomes of these surgeries is utilizing the robotics during orthopedic surgeries. Robot driving power, error potentials, and movement feasibility of the robots are the important parameters to increase the efficiency of robots. The special type of Yaskawa Motoman MH5 robot which is proposed in the present study can be useful to increase the workspace feasibility of this robot with optimal power to utilize during orthopedic surgeries. However, it is suggested in future studies to manufacture this robot and use it in the operating rooms for experimental evaluation of its clinical benefits.
Conclusion
In the present study, the transformation, spatial description, and movement of the Yaskawa Motoman MH5 robot were compared with two improved types of this robot. The results demonstrated that despite the fact that type A used less distance, this had a stronger possibility than type B for spatial movement and transformation. The first, second and third joints must be involved to create a static balance in type A robot, and for type B, in the same conditions, the first, second, third, and fourth joints must be involved. The orthopedic surgeries require great care and need to be performed with high sensitivity; the additional loading of type A robot loading difference may cause irreparable damages to patients and more wearing out of type A robot.
Conflicts of Interests
The authors declare no conflict of interest.
Authors’ Contributions
SZ and AE designed the study, data analysis, interpreted data, and wrote the final version of the manuscript. AE and AS collected the data, data analysis, and wrote the manuscript. All authors approved the final manuscript.
References
2. Gholampour S, Bahmani M, Shariati A. Comparing the efficiency of two treatment methods of hydrocephalus: shunt implantation and endoscopic third ventriculostomy. Basic and Clinical Neuroscience. 2019 May;10(3):185-98.
3. Gholampour S, Fatouraee N, Seddighi AS, Seddighi A. Evaluating the effect of hydrocephalus cause on the manner of changes in the effective parameters and clinical symptoms of the disease. Journal of Clinical Neuroscience. 2017 Jan 1;35:50-5.
4. Gholampour S, Seddighi A, Fatouraee N. Relationship between Spinal fluid and Cerebrospinal fluid as an index for assessment of non-communicating hydrocephalus. Modares Mechanical Engineering. 2015 Mar 11;14(13).
5. Gholampour S, Taher M. Relationship of morphologic changes in the brain and spinal cord and disease symptoms with cerebrospinal fluid hydrodynamic changes in patients with Chiari malformation type I. World Neurosurgery. 2018 Aug 1;116:e830-9.
6. Gholampour S, Gholampour H. Correlation of a new hydrodynamic index with other effective indexes in Chiari I malformation patients with different associations. Scientific Reports. 2020 Sep 28;10(1):1-3.
7. Khademi M, Mohammadi Y, Gholampour S, Fatouraee N. The nucleus pulpous of intervertebral disc effect on finite element modeling of spine. International Clinical Neuroscience Journal. 2016 Dec 7;3(3):150-7.
8. Gholampour S, Soleimani N, Karizi FZ, Zalii AR, Masoudian N, Seddighi AS. Biomechanical assessment of cervical spine with artificial disc during axial rotation, flexion and extension. International Clinical Neuroscience Journal. 2016 Sep 22;3(2):113-9.
9. Gholampour S, Soleimani N, Zalii AR, Seddighi A. Numerical simulation of the cervical spine in a normal subject and a patient with intervertebral cage under various loadings and in various positions. International Clinical Neuroscience Journal. 2016 Sep 22;3(2):92-8.
10. Gholampour S. FSI simulation of CSF hydrodynamic changes in a large population of non-communicating hydrocephalus patients during treatment process with regard to their clinical symptoms. PloS One. 2018 Apr 30;13(4):e0196216.
11. Gholampour S. Computerized Biomechanical Simulation of Cerebrospinal Fluid Hydrodynamics: Challenges and Opportunities. Computer Methods and Programs in Biomedicine. 2021 Mar;200:105938.
12. Gholampour S, Fatouraee N, Seddighi AS, Yazdani SO. A Hydrodynamical Study to propose a numerical Index for evaluating the CSF conditions in cerebralventricular system. International Clinical Neuroscience Journal. 2014 Aug 5;1(1):1-9.
13. Gholampour S, Fatouraee N, Seddighi AS, Seddighi A. Numerical simulation of cerebrospinal fluid hydrodynamics in the healing process of hydrocephalus patients. Journal of Applied Mechanics and Technical Physics. 2017 May;58(3):386-91.
14. Gholampour S, Bahmani M. Hydrodynamic comparison of shunt and endoscopic third ventriculostomy in adult hydrocephalus using in vitro models and fluidstructure interaction simulation. Computer Methods and Programs in Biomedicine. 2021 [in press].
15. Gholampour S, Fatouraee N. Boundary conditions investigation to improve computer simulation of cerebrospinal fluid dynamics in hydrocephalus patients. Communications Biology. 2021 [in press].
16. Taher M, Gholampour S. Effect of ambient temperature changes on blood flow in anterior cerebral artery of patients with skull prosthesis. World Neurosurgery. 2020 Mar 1;135:e358-65.
17. Hajirayat K, Gholampour S, Sharifi I, Bizari D. Biomechanical simulation to compare the blood hemodynamics and cerebral aneurysm rupture risk in patients with different aneurysm necks. Journal of Applied Mechanics and Technical Physics. 2017 Nov;58(6):968-74.
18. Gholampour S, Mehrjoo S. Effect of bifurcation in the hemodynamic changes and rupture risk of small intracranial aneurysm. Neurosurgical Review. 2020 Aug 16:1-0.
19. Hajirayat K, Gholampour S, Seddighi AS, Fatouraee N. Evaluation of blood hemodynamics in patients with cerebral aneurysm. International Clinical Neuroscience Journal. 2016 Jul 9;3(1):44-50.
20. Gholampour S, Hajirayat K. Minimizing thermal damage to vascular nerves while drilling of calcified plaque. BMC Research Notes. 2019 Dec;12(1):338.
21. Gholampour S, Jalali A. Thermal analysis of the dentine tubule under hot and cold stimuli using fluid– structure interaction simulation. Biomechanics and Modeling in Mechanobiology. 2018 Dec;17(6):1599-610.
22. Gholampour S, Gholampour H, Khanmohammadi H. Finite element analysis of occlusal splint therapy in patients with bruxism. BMC Oral Health. 2019 Dec;19(1):205.
23. Naghibzadeh M, Gholampour S, Naghibzadeh M, Sadeghian-Nodoushan F, Nikukar H. The effect of electromagnetic field on decreasing and increasing of the growth and proliferation rate of dermal fibroblast cell. Dermatologic Therapy. 2020 Jul;33(4):e13803.
24. Sedaghat Y, Gholampour S, Tabatabai Ghomshe F. Comparison of the effectiveness of manual cleaning, hydrogen peroxide vapour and ultraviolet-c in disinfection of hospital equipment. Infektološki Glasnik. 2019;39(3):66-84.
25. Hassanalideh HH, Gholampour S. Finding the optimal drill bit material and proper drilling condition for utilization in the programming of robot-assisted drilling of bone. CIRP Journal of Manufacturing Science and Technology. 2020 Nov 1;31:34-47.
26. Roche MW, Augustin D, Conditt MA. Accuracy of robotically assisted UKA. InOrthopaedic Proceedings 2010 Mar (Vol. 92, No. SUPP_I, pp. 127-127). The British Editorial Society of Bone & Joint Surgery.
27. Cobb J, Henckel J, Gomes P, Harris S, Jakopec M, Rodriguez F, et al. Hands-on robotic unicompartmental knee replacement: a prospective, randomised controlled study of the acrobot system. The Journal of Bone and Joint Surgery. British Volume. 2006 Feb;88(2):188-97.
28. Musahl V, Plakseychuk A, Fu FH. Current Opinion on Computer-Aided Surgical Navigation and Robotics. Sports Medicine. 2002 Nov;32(13):809-18.
29. Gholampour S, Deh HH. The effect of spatial distances between holes and time delays between bone drillings based on examination of heat accumulation and risk of bone thermal necrosis. Biomedical Engineering Online. 2019 Dec;18(1):65.
30. Vahdat I, TabatabaiGhomsheh F, Gholampour S, Rostami M, Khorramymehr S. Biomechanical evaluation of passive resistive torque structure of elbow joint and its application in rehabilitation and practical equipment. Journal of Modern Rehabilitation. 2015 Nov 10;9(4):16- 24.
31. Shariati A, Shamekhi AH, Ghaffari A, Gholampour S, Motaghed A. Conceptual Design Algorithm of a. Two-Wheeled Inverted Pendulum Mobile Robot for Educational Purposes. Mechanics of Solids. 2019 Jul 1;54(4):614-21.
32. Sheikh R, Gholampour S, Fallahsohi H, Goodarzi M, Taheri MM, Bagheri M. Improving the efficiency of an exhaust thermoelectric generator based on changes in the baffle distribution of the heat exchanger. Journal of Thermal Analysis and Calorimetry. 2021 Jan;143:523-33.
